#011 Test AB con Python (III) - Exploratory Data Analysis
Sí, lo sé.
Hace mucho tiempo que no escribo y pido disculpas por dejar esta trilogía a la mitad desde hace tanto tiempo. No hay excusas más allá del foco en otras áreas de mi vida, pero el momento ha llegado:
En esta 11ª edición finaliza la trilogía sobre Python y su relación con AB testing. A continuación, nos introduciremos en un proceso paso a paso que seguimos en LIN3S para la interpretación de datos con Python.
Ahora sí, empieza Test AB con Python (III): Exploratory Data Analysis.
Espero que os guste.
Los puntos de esta edición:
Importancia del análisis de datos en AB testing
Proceso de diagnóstico pàra tests AB
Definición de tipología de datos
Definición de hipótesis y por qué importa
Carga de datos
EDA: Exploratory Data Analysis
Evaluación de distribución
Ejecución del test estadístico
Epílogo de la trilogía
Importancia del análisis de datos en AB testing
Ya he contado en algunas formaciones y webinars un suceso que tuve a principios de 2022 cuando todo lo que podía salir mal, salió mal. Se trataba de un split test con dos versiones, nada que no hubiera hecho antes.
Como se ve en la imagen, calculé la p-valor de este test y resultaba muy prometedor al ser menor a 0.05, es decir, podíamos inferir que existía significancia estadística y que la variante se podía lanzar a producción.
O eso creía…
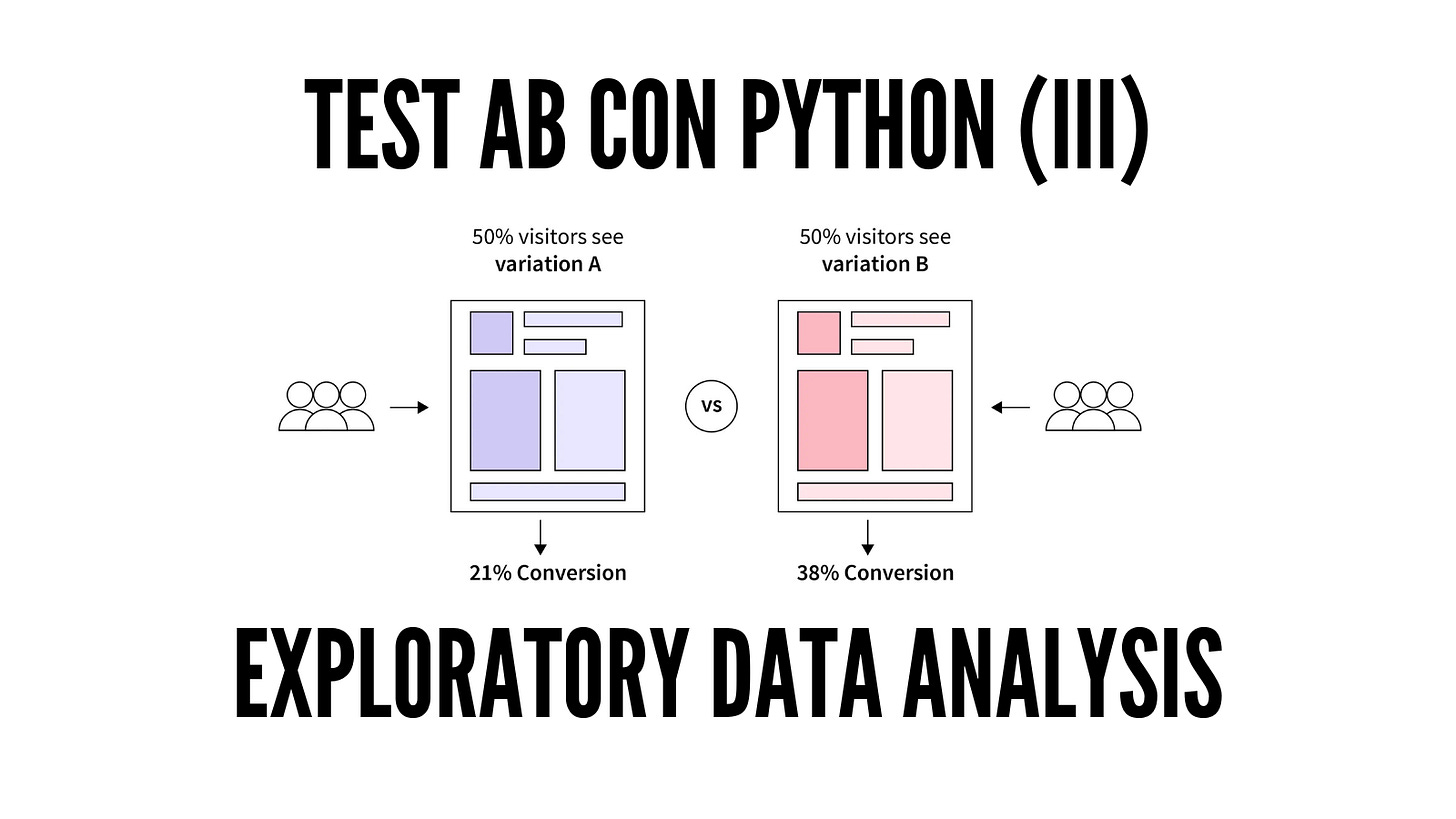
Sin embargo, ahondé un poco más y casi por accidente di con este boxplot, desde luego, a simple vista, ya se ve que algo no funciona como debería:
Esas “bolitas” que tiene la variante son outliers, es decir, valores atípicos. Estos no deben preocuparnos especialmente en el marco de un test AB ya que, se supone, su distribución debería ser homogénea entre los dos grupos (control y variante). Sin embargo, aquí vemos que la inmensa mayoría de valores atípicos se había ido a la variante.
¿Qué había pasado?
En resumen, el equipo de marketing de esta empresa —estaba como consultor freelance por aquél entonces— había enviado tráfico directamente a la URL de la variante en unas promociones concretas.
La promoción aumentó las conversiones.
Estos usuarios “no podían” dirigirse al grupo de control ya que se les enviaba directamente a la URL de la variante.
Como sucedió a lo largo de una semana (un poco largo) el cálculo de la p-valor no pudo salvar estos datos atípicos.
Además, no saltó el aviso de SRM de la herramienta de testing.
Es decir, todo lo malo que podía pasar, pasó.
¿Qué hice?
Se decidió repetir el test, pero aproveché para eliminar las ventas de ese periodo con outliers para calcular la p-valor. El resultado lo tienes en la siguiente imagen y fue muy similar cuando se repitió el experimento. Es decir, se pasó de una significancia estadística indiscutible a favor de la variante a unos datos, con el segundo test, que no auguraban un impacto en el negocio.
Esta es la razón por la que pienso que debe haber un proceso de exploración de datos previo al cálculo de la p-valor. No entender las características de la distribución de tus datos únicamente hará que tomes peores decisiones y que caigas en los falsos positivos y falsos negativos.
En esta edición te quiero enseñar un proceso de trabajo para que esto no te pase.
Proceso de diagnóstico para tests AB
1. Definición de tipología de datos
No todos los datos son iguales. En muchas ocasiones, en marketing digital, tratamos a revenue y a transacciones y eso es un error. La tipología de dato no solo determina en ocasiones el tipo de test que ejecutarás, sino también la manera de visualizarlo y del tratamiento que debes darle.
En AB testing, habitualmente, nos enfocamos en:
Datos discretos: En general, son números enteros.
Ejemplo: Número de transacciones, clicks, leads generados, entre otros.
Con este tipo de dato se usa habitualmente t-test (cuando la muestra es grande ya que el t-test debe ejecutarse con datos continuos), regresión de Poisson cuando sigue una distribución de Poisson, mann-whitney U cuando es un test AB con distribucción no paramétrica y ANOVA o Kruskal-Wallis cuando es un ABC/n test con distribución normal.
Datos continuos: En general, son decimales o fracciones. Pueden tomar cualquier valor dentro de un rango.
Ejemplo: Revenue, Tiempo en página, ARPU
Con este tipo de dato se usa habitualmente t-test, mann-whitney U cuando es un test AB y ANOVA o Kruskal-Wallis cuando es un ABC/n test
Categóricos nominales: Son aquellos que representan una categoría o tag y NO tienen un orden numérico.
Ejemplo: Categoría de dispositivo (es decir, mobile, desktop, tablet...), Fuente/medio del usuario (organic/google, paid/google...)
Con este tipo de dato se usa habitualmente:
Con muestra grande: Chi-squared (en algún caso, se puede usar G-test de independencia)
Con muestra pequeña: Fischer's exact test
Categóricos ordinales: Son aquellos que representan una categoría o tag y SÍ tienen un orden implícito.
Ejemplo: Puntuación de una encuesta (muy satisfecho, satisfecho, poco satisfecho, muy poco satisfecho).
Con este tipo de dato se usa habitualmente:
2 grupos: Mann-Whitney U
3 grupos o más: Kruskal-wallis
Como puedes ver, estamos mencionando muchos tipos de test, pero, ¿qué es exactamente todo esto?
Un error muy común en AB testing es utilizar las calculadoras en línea para calcular la p-valor, pero como se puede deducir, estas utilizan un método único para devolver la p-valor (habitualmente z-test o t-test), sin embargo, el tipo de test que ejecutes te devolverá una p-valor u otra, modificando, a veces en gran medida, tu diagnóstico.
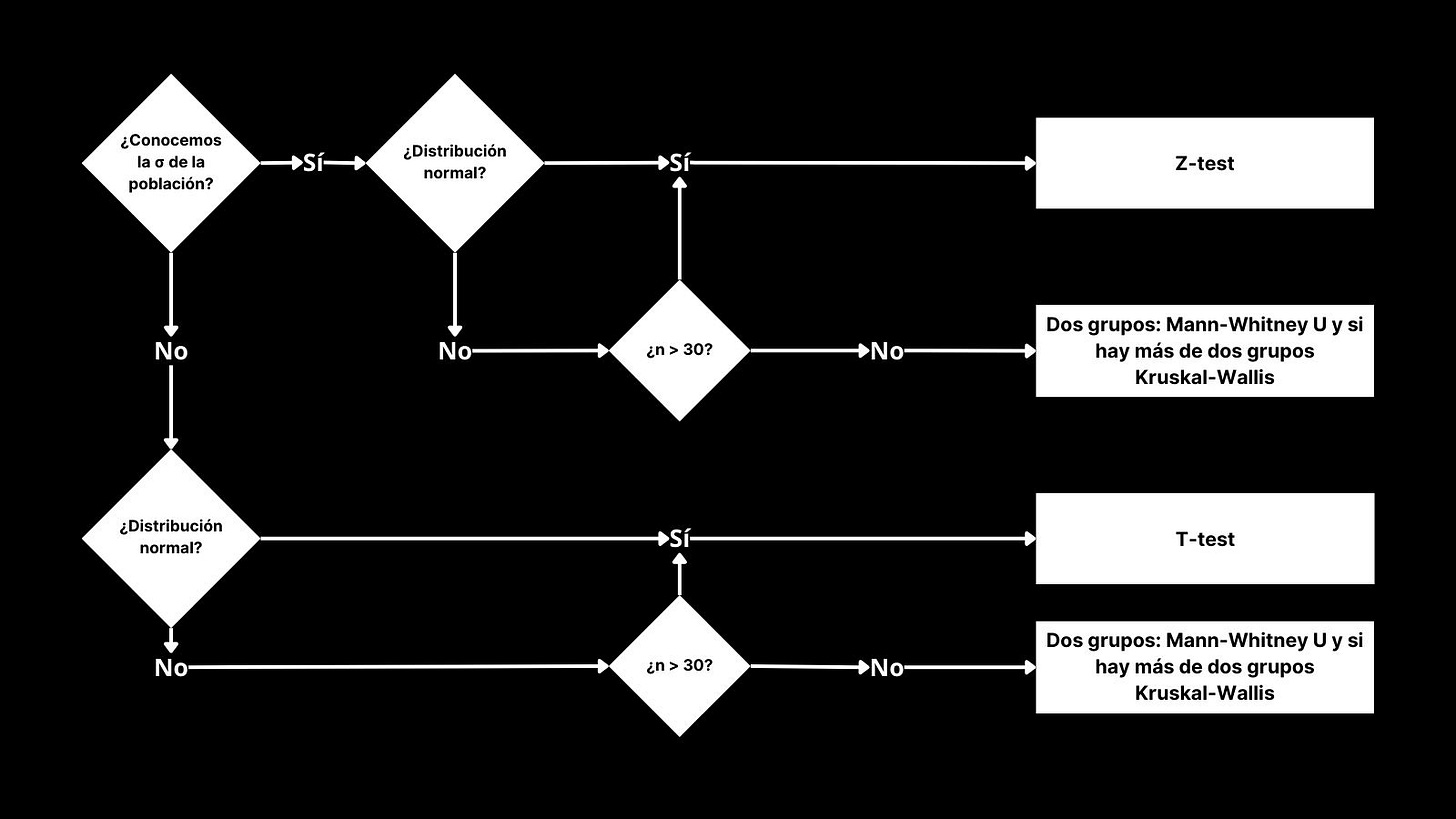
Es por ello que debes seguir un proceso que te ayude a seleccionar qué clase de diagnóstico ejecutar. Como se puede ver, hay más elementos además de la tipología de datos que determinan el tipo de test y vamos a continuar con los siguientes pasos una vez vistos los tipos de datos y los tipos de tests que pueden ser más habituales.
2. Definición de hipótesis
¿De verdad es tan importante definir la hipótesis? ¿En qué cambiará mi resultado escribir o no la hipótesis? Más allá de lo importante que es seguir un proceso o el hecho de que definir una hipótesis ayuda a ordenar tu pensamiento y especialmente tus métricas primarias, hay un factor técnico que a veces se olvida.
Existen tipos de hipótesis: one-tailed y two-tailed.
Si armamos una hipótesis con esta estructura básica estaremos armando una hipótesis one-tailed, la más típica en CRO ya que a menudo hacemos tests para aumentar una métrica:
Hipótesis alternativa (H1): Si _____ entonces aumentará la métrica objetivo.
Hipótesis nula (H0): Si ____ entoneces no aumentará la métrica objetivo.
Sin embargo, si armáramos una two-tailed sería así:
Hipótesis alternativa (H1): Si _____ entonces la métrica objetivo será superior o inferior.
Hipótesis nula (H0): Si ____ entoneces no aumentará la métrica objetivo.
¿Hay visto la diferencia? en la H1 indica que será superior o inferior, es decir, diferente a la hipótesis nula. Esto es importante porque determina la naturaleza del test y sobre todo el resultado de la p-valor. Bien puedes verlo en la calculadora en línea de test AB y comparar los resultados entre one-sided y two-sided.
Es decir, definir el tipo de hipótesis determina si debes escoger un sub-tipo de test: los de una cola o los de dos colas.
3. Cargar los datos
Hay libros enteros dedicados a esta subsección del proceso de diagnóstico, ya que cubriría toda la parte relacionada con carga, transformación de datos, data wrangling, entre otros.
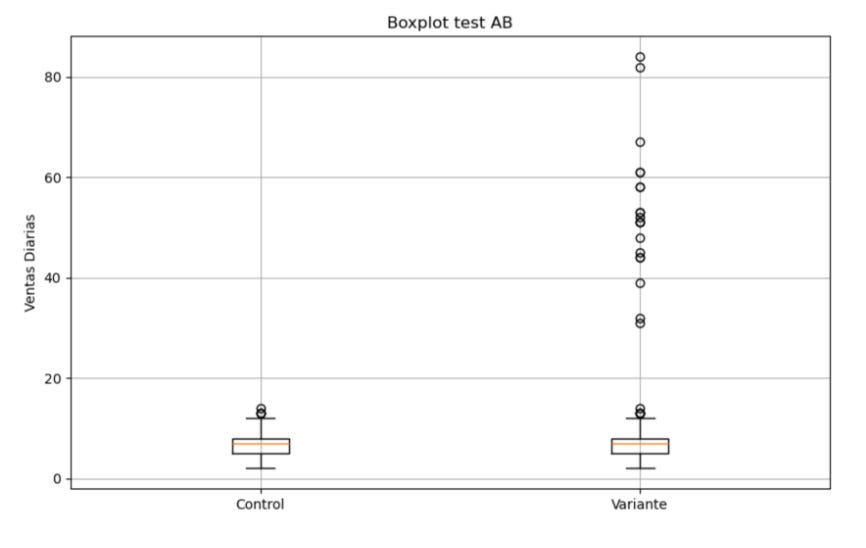
De alguna manera, al final este paso deberíamos tratar de obtener algo tal que así si hiciéramos un test AB en el que queremos medir impacto en transacciones y revenue:
Es fundamental destacar la importancia de la calidad del dato: no se puede hacer CRO sin una calidad mínima.
4. EDA: Exploratory data analysis
Como ya sabemos, es fundamental antes de calcular la p-valor hacer una descripción de la distribución de los datos. En algunos tests AB deberá ser más concienzuda y en otros menos, ya que dependerá del tipo de test, la sección de la web/app que manipulemos, entre otros.
Esta fase es útil para, por ejemplo, detectar valores atípicos (outliers) y entender mejor a qué dataset nos estamos enfrentando. Sin embargo, esta fase no es tan simple, ya que en función del tipo de datos que tengamos deberemos usar una serie de visualizaciones u otras (por eso el paso 1 es tan determinante).
Para simplificar esto, nos centraremos en datos continuos y discretos, ya que son los mayores protagonistas en evaluación de tests AB.
4.1 Situación A: Datos continuos (revenue)
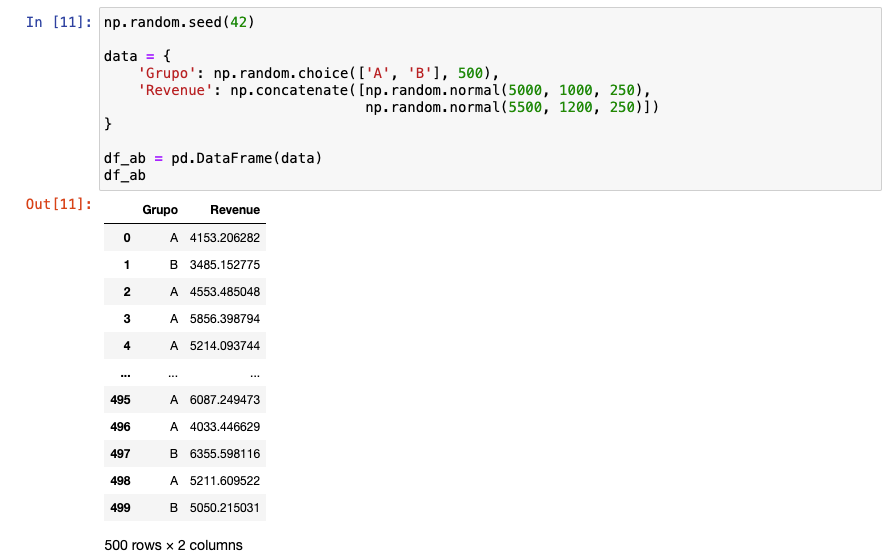
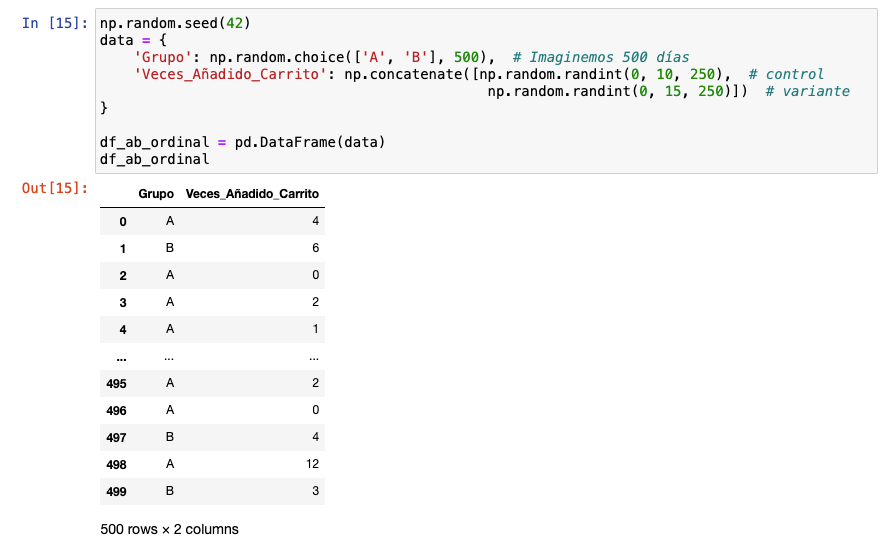
Montamos un dataset básico ccon 500 registros. Recuerda que si usas pd.read_scv(“file.csv”) puedes cargar datos de CSV procedentes, por ejemplo, de una exploración de GA4.
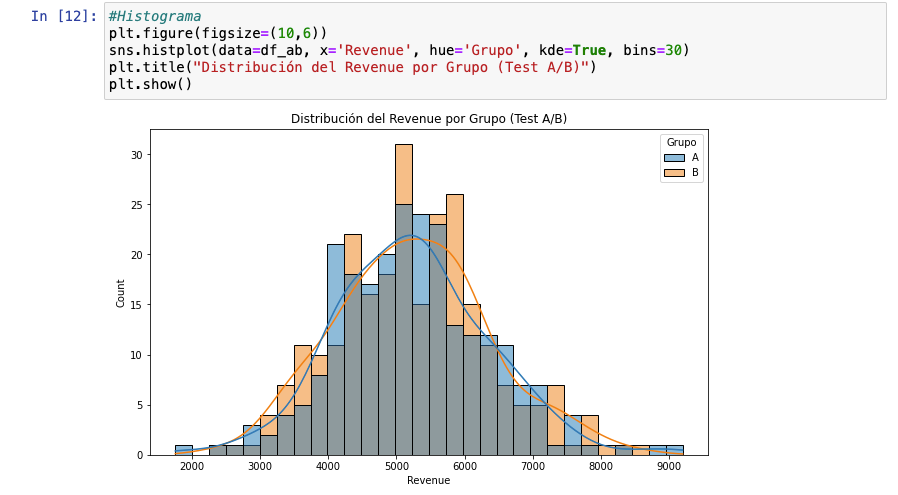
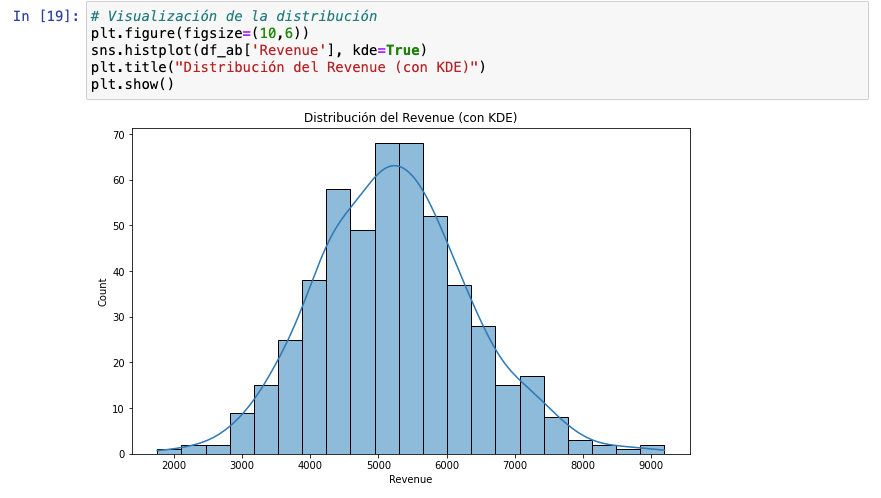
Con datos continuos es recomendable no usar gráficos de barras, sino en su lugar hacer uso de un histograma. Aquí tienes un ejemplo. Verás que el histograma y el Kernel Density Estimate (kde) serán principales aliados para el paso 5.
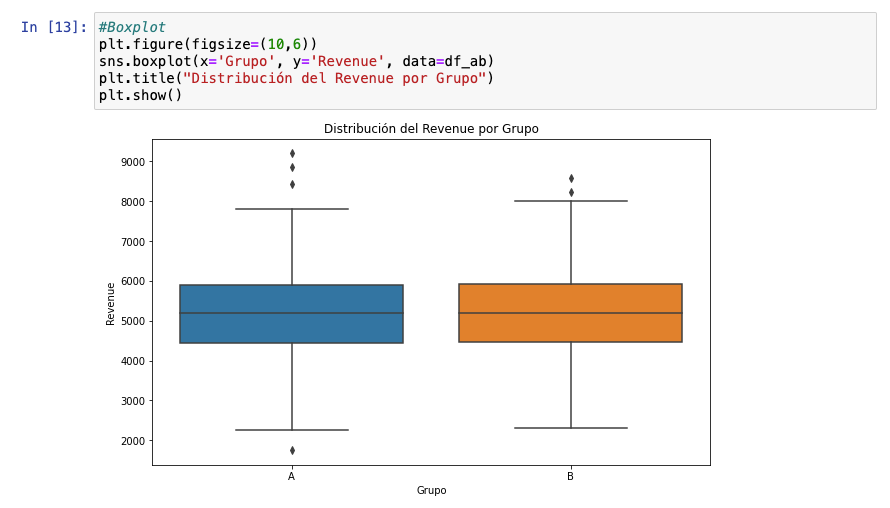
Otro tipo de visualización muy útil para datos continuos y discretos es también el boxplot. Me declaro muy fan de esta visualización porque creo que no existe ninguna gráfica que enseñe tanto en tan poco espacio.
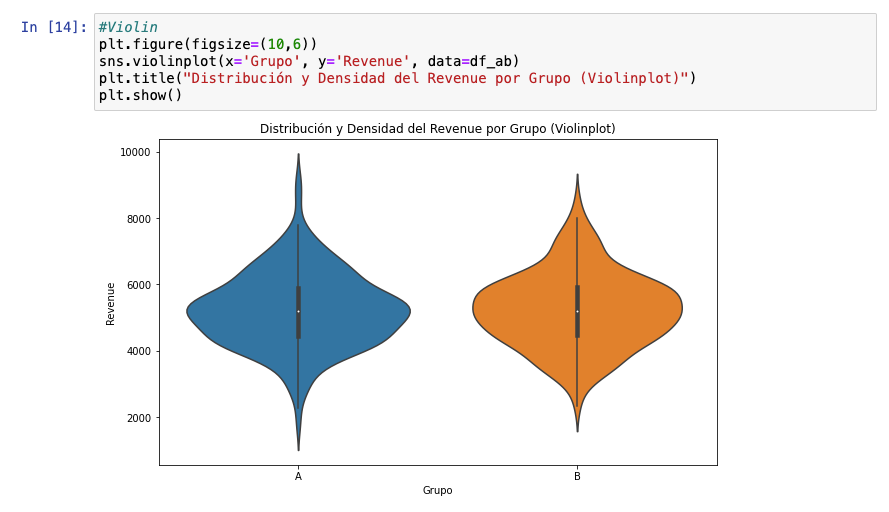
Un primo hermano del diagrama de caja es el de violín, que si bien añade una camap más visual de información con su forma, debe reconocer que no me gusta tanto (a gustos colores). No obstante, no se puede negar su potencial.
Con estos tipos de visualizaciones podemos hacernos a la idea de la distribución de los datos. Por ejemplo, podemos saber que son dos grupos bastante similares aunque el grupo de control ha sumado más valores atípicos que la variante (lo cual no es necesariamente malo). Probablemente, no exista significancia estadística a favor de la variante, pero debemos seguir con el análisis.
4.2 Situación B: Datos discretos (add to carts)
Repetimos la operación, sin embargo, debemos tener en cuenta que estos tienen característicass diferentes. Por ejemplo, no es recomendable hacer uso de histograma con ellos y es más habitual utilizar gráficos de barras.
Cargamos los datos con estos datos ficticios:
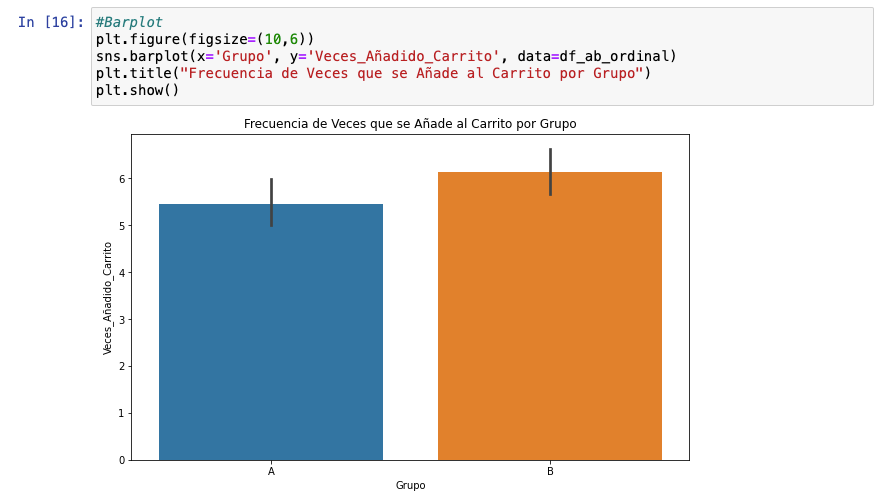
Ejecutamos un barplot. Se vislumbra de forma visual que la variante funciona mejor que el grupo de control. Es interesante entender y ver que el tipo de dato determina el tipo de visualización porque será fundamental para interpretar el tipo de distribución en el siguiente paso.
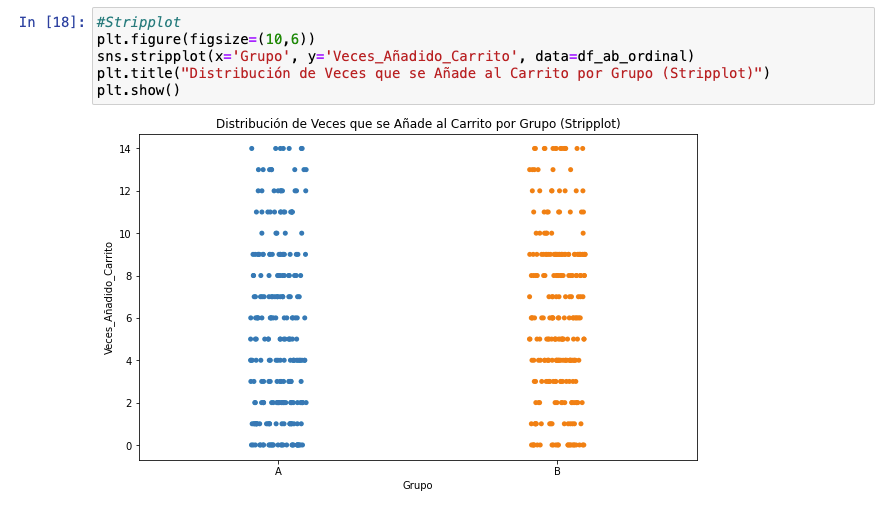
En esta fase, podemos trabajar con gráficas similares, pero quiero aprovechar para mostrar una visualización infra-utilizada: el stripplot, que es útil para observar la distribución de puntos (valores) dentro de las categorías que estás comparando.
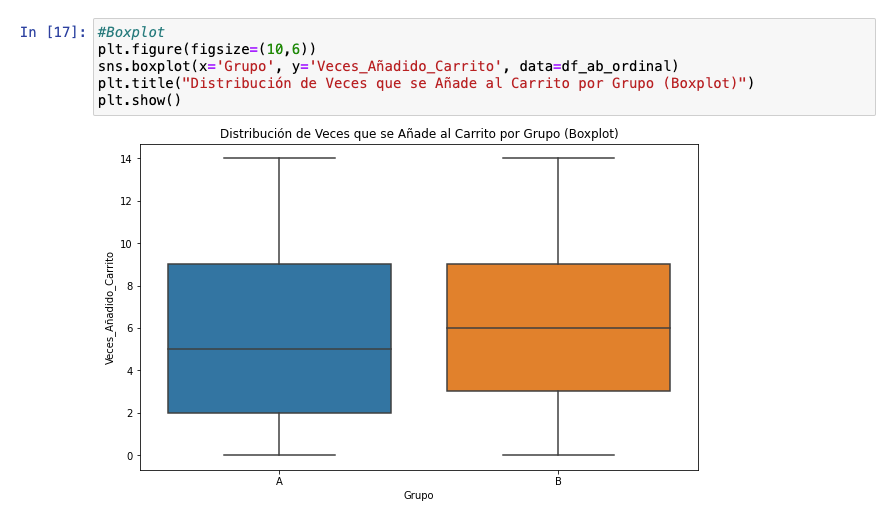
Y cómo no, el boxplot, como he dicho soy muy fan. Podemos ver que es similar salvo que la mediana es superior en la variante. ¿Puede ser eso suficiente para ser estadísticamente significativo? Eso deberemos verlo calculando la p-valor, pero para ello debemos saber qué test usar, lo que viene determinado, también, por el tipo de distribución de datos.
5. Evaluación de distribución
Evaluar qué clase de distribución tenemos es particularmente importante, ya que de ello depende qué clase de test ejecutar para evaluar si tenemos significancia estadística o no. No obstante, la manera de evaluar qué clase de distribución tenemos también depende del tipo de dato, así que veremos a continuación cómo encarar este tema.
5.1 Datos continuos (revenue)
Aquí mostraremos el histograma con KDE, es decir, con Kernel Density Estimate.
Esto lo usamos para mostrar cómo los datos se distribuyen en el eje de valores, proporcionando una idea clara de dónde se concentran los valores. Esto es útil para identificar los modos (picos en la distribución) y para ver la forma de la distribución de los datos (simétrica, sesgada, etc.).
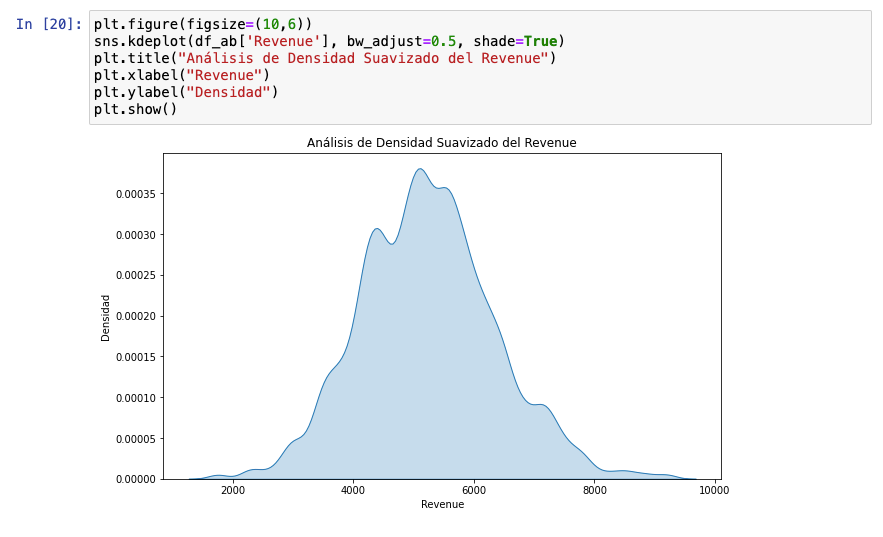
En este caso, vemos que hay dos barras que están unidas en un mismo punto. Podríamos pensar que se trata de una distribución bimodal ligera, por eso, ejecutamos el siguiente gráfico:
Viendo este gráfico, podemos advertir que no es unimodal. No obstante, si quieres asegurarte, puedes ejecutar este código con Hartigan’s Dip Test:
Una manera adicional de diagnósticar qué clase de distribución tenemos es mediante skewness y kurtosis para entender la asimetría (skewness) y el grado de valores atípicos que tenemos (kurtosis).
Después, aplicaríamos Shapiro-Wilk test o Kolmogorov-Smirnov para definir si tenemos o no una distribución normal, cosa fundamental como vimos en el diagrama inicial de toma decisiones.
Aquí el cálculo de skewness y kurtosis
Skewness: 0 es perfectamente simétrico
0.23 indica unaligera asimetría positiva, lo que significa que la cola derecha de la distribución es un poco más larga o más pesada que la izquierda. En otras palabras, hay algunos valores de revenue altos que están arrastrando la cola derecha, pero no de manera extrema.
Kurtosis: 3 sería una distribución normal (mesocúrtica)
3.30 indica que la distribución tiene un ligero apuntamiento mayor que la normal (leptocúrtica).
Y a continuación, con Shapiro podemos ver que se trata de una distribución normal ya que la p-valor es mayor a 0.05:
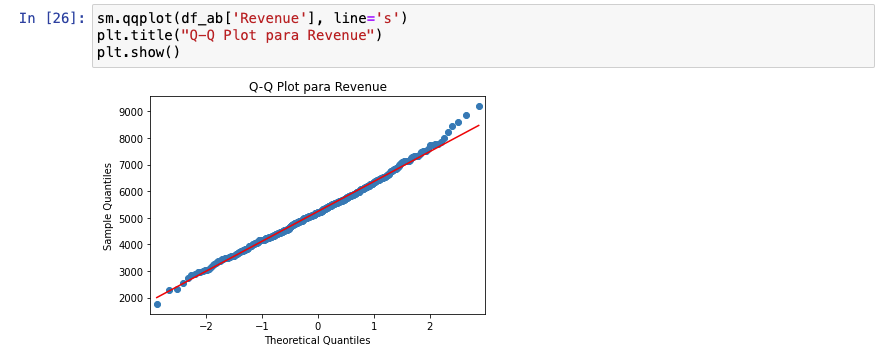
Una cosa interesante que puede añadirse a este análisis de la distribución es un Q-Q Plot, que permitiría evaluar cómo la distribución de nuestro dataset es fidedigna a una distribución normal téórica. En nuestro caso:
La línea de puntos está encima de la línea roja salvo en los extremos. Esto es un caso muy típico en métricas como revenue. Esto significa que podría haber outliers pero como vimos en el anterior paso (EDA), si existen, probablemente estén perfectamente distribuidos en ambos grupos.
Existen métodos como z-score e IQR para averiguar cuáles son específicamente esos outliers a los que apunta el Q-Q plot, sin embargo, en este contexto, no sería necesario y forma parte de un análisis de otro tipo. En siguientes ediciones profundizaremos en regresiones y análisis estadístico avanzado.
Nuestro diagnóstico: Disponemos de una distribución normal, por lo que podemos usar tests paramétricos. Probablemente, t-test sea la mejor opción.
5.2 Datos discretos (add to carts)
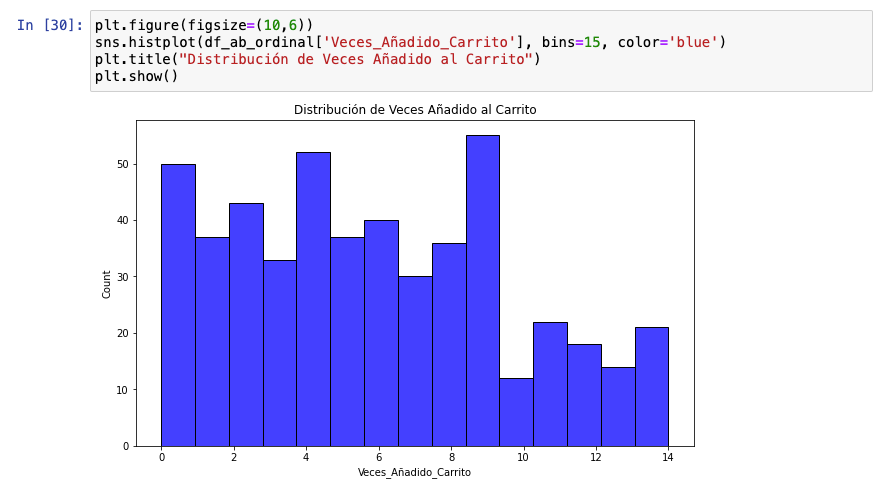
Como dijimos en anteriores secciones, los datos discretos son distintos a los continuos. Tanto es así que si ejecutamos un histograma, nos encontramos con esto:
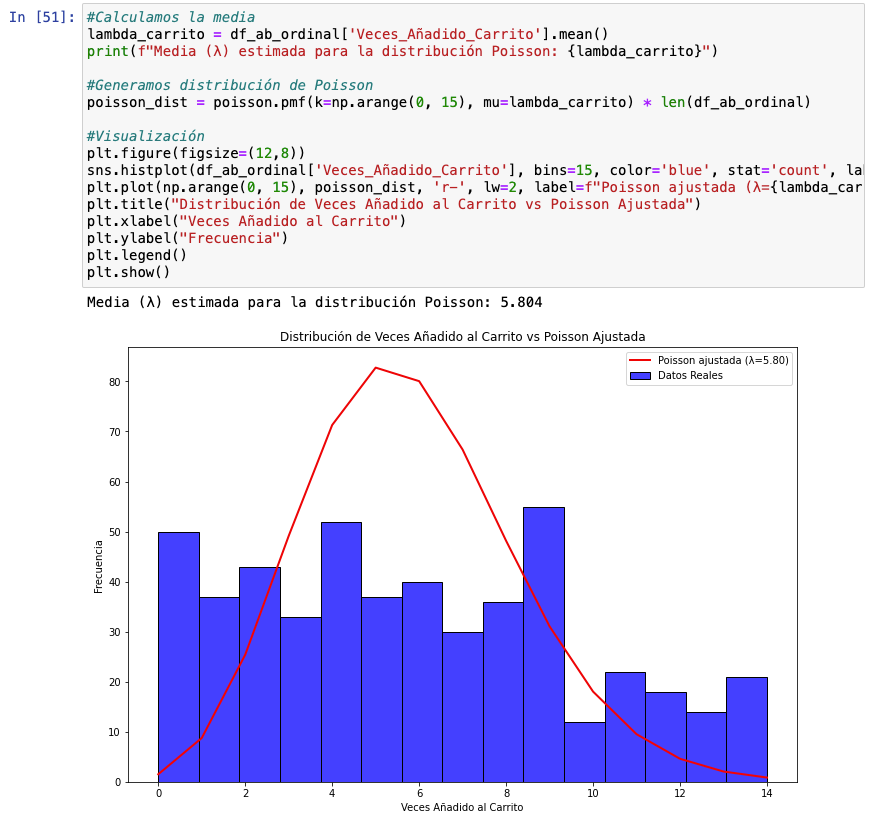
¿Qué clase de distribución es esto? Pues bien, con datos discretos es habitual encontrarte cosas así, especialmente en marketing digital. Por ello, trabajar una distribución de Poisson cuando tenemos datos discretos y ver si encaja con este tipo de datos es lo que debemos hacer a diferencia de con los datos continuos.
¿Qué hacemos en el siguiente gráfico? Calculamos la media (que en el contexto de Poisson se hace llamar lambda) ya que en Poisson la media y la varianza son equivalentes y evaluamos si esta línea ajustada a la media encaja con nuestros datos reales.
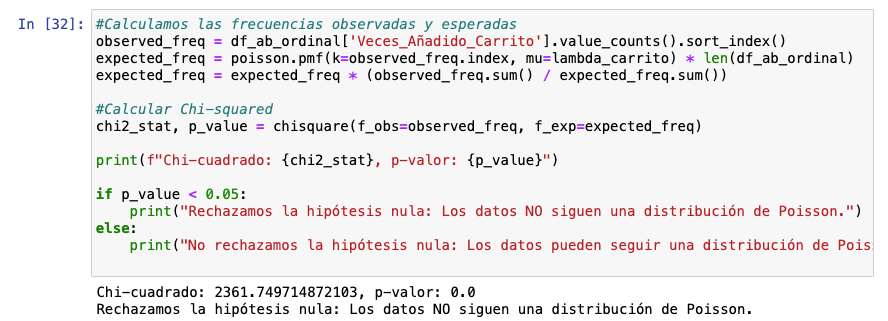
Como podemos ver en este gráfico, en absoluto encajan. No obstante, con chi-squared aplicando un test de bondad de ajuste podríamos verlo con números. No, no sigue una distribución de Poisson.
¿Qué hacemos ahora? Habría que bucear y ver qué clase de distribución es esta. Un paso habitual es evaluar si tenemos una distribución binomial negativa, pero creo que queda claro que tenemos una distribución apta para tests no paramétricos en cuyo caso, Mann-Whitney U es interesate.
6. Ejecución del test
6.1 Datos continuos (revenue)
Como puede verse, nuestra variante no resultó ser la ganadora (p-valor = 0.5313).
6.2 Datos discretos (add to carts)
Como puede verse, nuestra variante sí resultó ser la ganadora (p-valor = 0.0192).
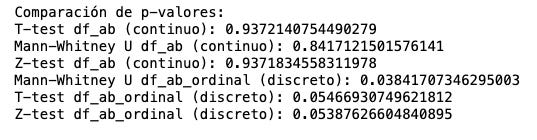
¿Qué pasaría si ejecutamos otros tests con estos mismos datos? He hecho la prueba y especialmente sangrante con p-valor pequeñas. Si hubieras usado t-test o z-test con los datos discretos te habría dado como perdedora la variante, por lo que habrías caído en un falso negativo.
El motivo por el que esto sucede es simple: Mann-Whitney se basa más en rangos y habitualmente resulta menos sensible a valores atípicos mientras que t-test, por ejemplo, se centra en medias. ¿Esto significa que Mann-Whitney es mejor? No. Sigifica que elegir el test es crítico para el éxito de tu proyecto de CRO.
7. Conclusión y Epílogo
Este proceso de diagnóstico muestra la profundidad que existe a la hora de diagnosticar un test AB. Me ha quedado largo y podría haber añadido aspectos de correcciones de Bonferroni ante comparaciones múltiples (Cosa crítica en CRO también y que tendrá su propio capítulo) o FDR.
Profundizar en la parte técnica y de datos de CRO es una de las cosas más sorprendentes que he vivido jamás. Cómo a través de datos podemos llegar a un nivel de tal abstracción. Un reto al que, sin duda, las organizaciones que quieran llegar lejos deberán recorrer.
¿Quieres profundizar en analítica de datos con Python y no sabes cómo empezar? He escrito un libro con Joseba Ruiz llamado “Analítica de datos con Python para marketing digital” que te ayudará a dar los primeros pasos en este mundo tan fascinantes.
May the CRO be with you.