CRO será técnico o no será.
Parece que a muchas personas les ha resonado esta frase que he ido repitiendo durante este año en algunos posts en LinkedIn y Twitter (me niego a llamarla X). Todo este afán por la técnica proviene de otra frase mía que no ha cuajado tanto porque quizás no la he voceado en los foros correctos: “El estratega deberá ser más analista y el analista más estratega”.
Leanalytics nace con el propósito de acercar ciertos elementos técnicos y bajarlos al suelo. En esta 15ª edición hablo de K-means, un algoritmo no supervisado muy conocido en el ámbito de la ciencia de datos que, sin duda, todo especialista en CRO o analista debería conocer.
Ahora sí, empieza K-means: de la teoría a la práctica.
Espero que os guste.
Esto es lo que vamos a ver en esta edición:
Qué es
La distancia o similitud
Linkage
Definición de k-means
K-means paso a paso
Cómo seleccionar k
Caso kaggle
Evaluación del modelo y caso y Caso GA4
¿Qué es K-means?
La distancia o similitud
Antes de nada, el agrupamiento no supervisado persigue un objetivo muy claro: identificar patrones o grupos en los datos basándose en la similitud de sus características. Esto se consigue a partir de:
Un conjunto de objetos descritos por un vector.
Una métricca que nos defina el concepto de “similitud”
Este concepto de similitud es fundamental. En esencia, es la forma de cuantificar cómo de similares son dos objetos, variables o puntos en el espacio. Consideraremos que habrá similitud cuando cualquier distancia contenga las tres condiciones siguientes:
No negatividad: la distancia siempre debe ser positiva.
Simetría: la distancia de la A la B debe ser la misma que de la B a la A.
Desigualdad triangular: la distancia debe coincidir con la idea de que es el camino más corto entre los dos puntos.
Con estas tres condiciones, tendremos la definición de lo que llamamos distancia o similitud.
Linkage
El principio de un algoritmo aglomerativo es que se obtienen todos los datos como algo individual hasta que se obtienen una serie de grupos, es decir, sucede el agrupamiento de objetos.
Para construir esos grupos se necesita entender el concepto de distancia y el concepto de enlace (linkage). Algunos de los criterios clave, son:
Simple linkage: Utiliza la distancia mínima. Muy sensible entonces al ruido en el dataset.
Complete linkage: Utiliza la distancia máxima. No es tan sensible al ruido en el dataset pero entonces es más sensible a los outliers. No obstante, puede dar en ocasiones mejores resultados que simple linkage.
Average linkage: Utiliza la distancia media. Es un método que intenta coger lo mejor de los dos anteriores y resolver sus problemas sin conseguirlo.
Centroid linkage: La distancia entre dos grupos será la distancia entre sus dos centroides. Es decir, la posición central de cada grupo.
Aunque K-means no utiliza directamente criterios de enlace como el simple, complete o average linkage, comparte el mismo principio de medir distancias para agrupar objetos similares. Sin embargo, en lugar de calcular distancias entre puntos o grupos, K-means utiliza un enfoque centrado en los centroides.
Un centroide es el punto medio de un grupo. Se calcula como la media de todas las características de los datos dentro del grupo. En cada iteración, K-means ajusta los centroides y reasigna los puntos al grupo más cercano, optimizando así la similitud dentro de cada grupo.
Definición de k-means
K-means es un algoritmo de agrupamiento no supervisado que sirve para dividir un dataset en "clusters" basados en las similitudes de sus características. A diferencia de otros métodos, este algoritmo requiere que decidas previamente cuántos grupos (k) quieres formar.
Por ejemplo, si estás segmentando clientes en función de su comportamiento de compra, podrías elegir dividirlos en tres grupos (k=3): compradores frecuentes, ocasionales y nuevos. El algoritmo, entonces, identificará los grupos asignando cada cliente al grupo más cercano, calculado en función de su posición en el espacio de datos.
K-means paso a paso
1. Seleccionar K
Antes de comenzar, seleccionaremos el número de clusters k, que determina cuántos grupos queremos identificar en los datos.
2. Calcular centroides
Asignaremos cada observación xi al cluster Ct cuyo centroide inicial ct esté más cerca, según una métrica de distancia (por ejemplo, la distancia centroide).
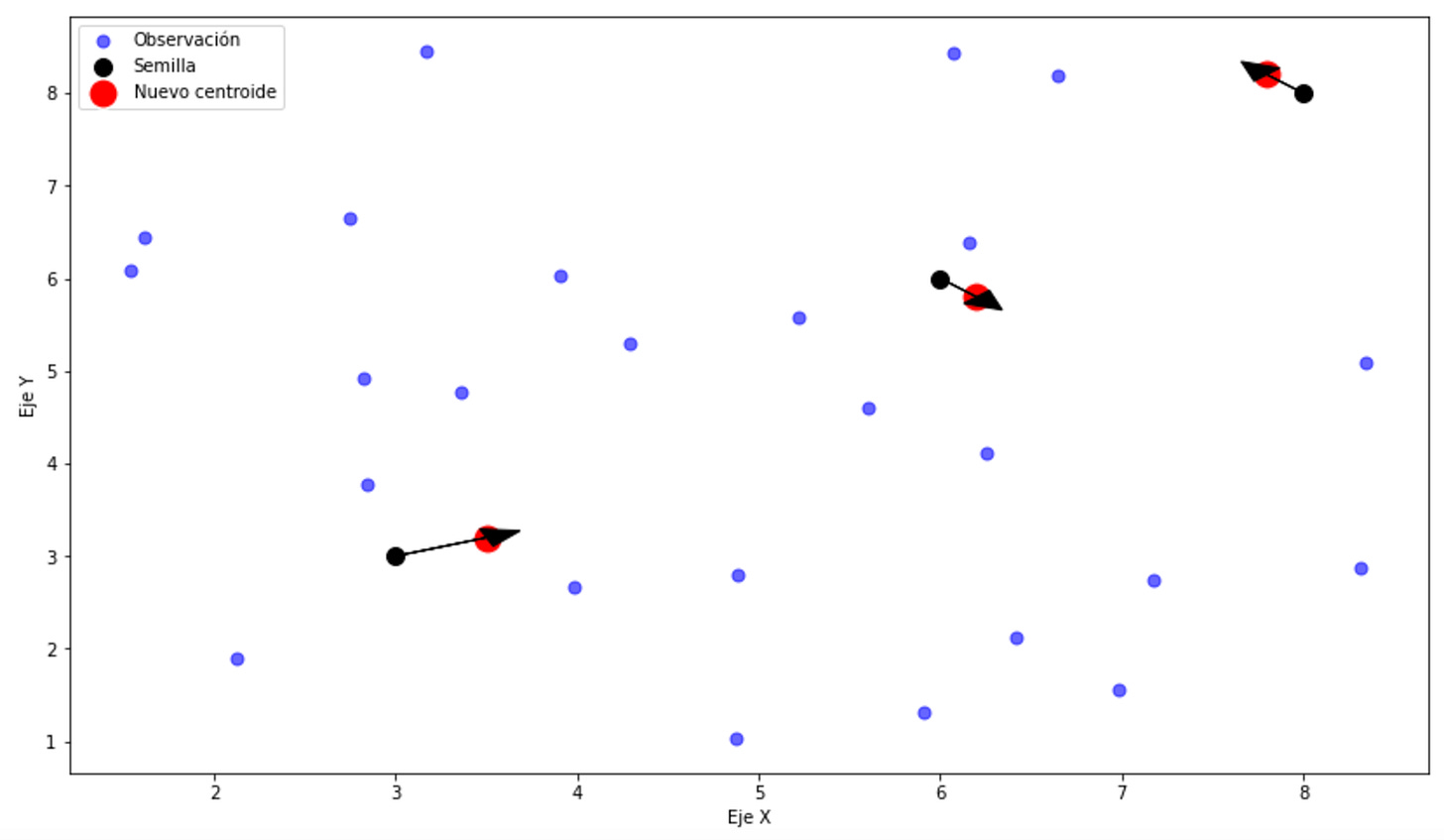
3. Nuevo cálculo
Una vez que las observaciones han sido asignadas a sus respectivos clusters, recalcularemos los centroides de cada cluster como el promedio de las observaciones asignadas.
4. Criterio de parada y cambio
Como criterio de parada, evaluaremos si las asignaciones de las observaciones a los clusters han cambiado. El algoritmo finalizará cuando los cambios sean mínimos o cuando la suma de las distancias cuadradas dentro de los clusters deje de mejorar significativamente.
5. Repetir
Repetiremos los pasos 2, 3 y 4 hasta que los clusters se estabilicen y ya no haya cambios significativos en las posiciones de los centroides.
Cómo seleccionar k
Puede ser común pensar que k puede escogerse de forma arbitraria, pero no tiene por qué ser así. De hecho, la manera idónea es escoger el número de k óptimo en función de las caracter´sticacs del dataset.
El más conocido es el método Elbow, que te presento a continuación:
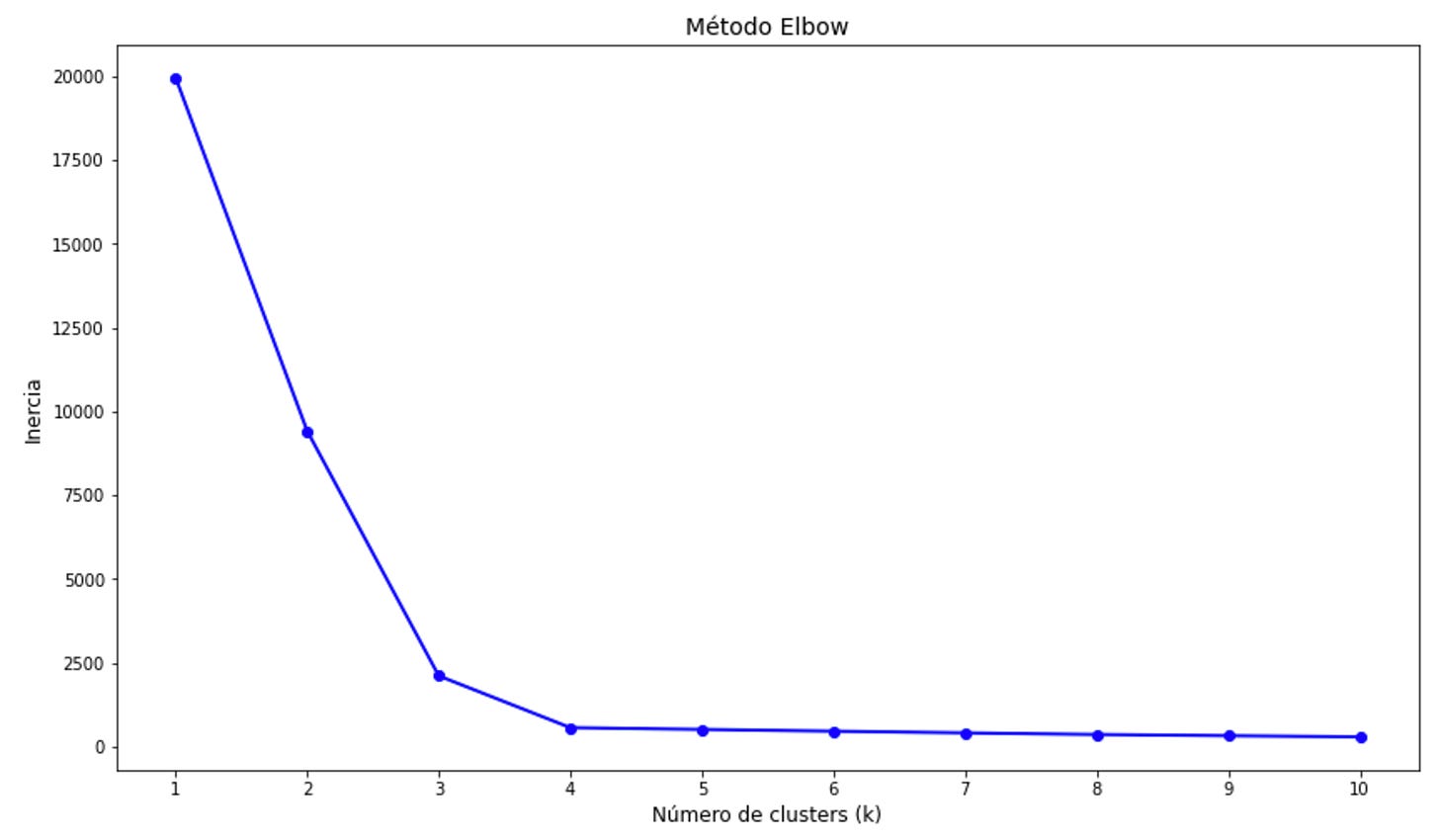
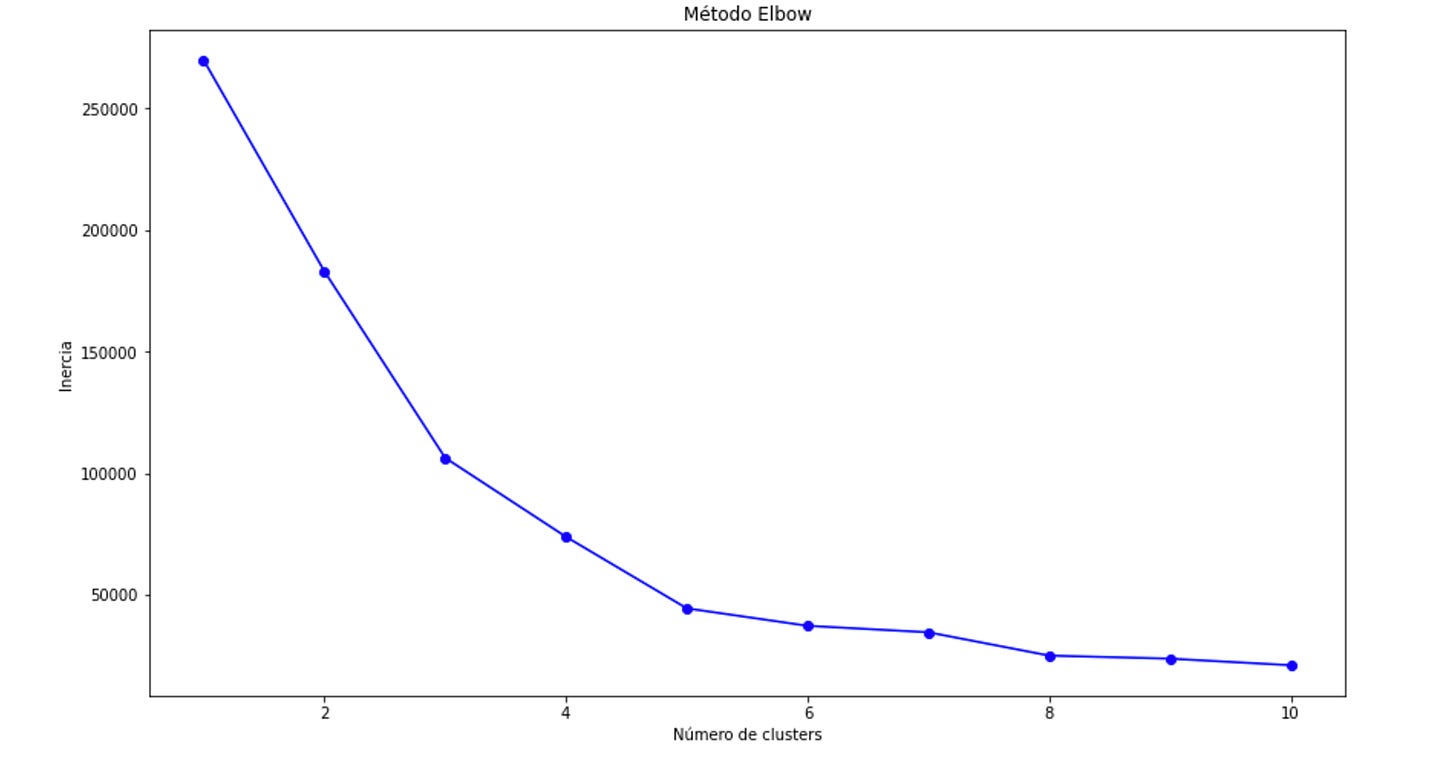
El método Elbow es una técnica que se utiliza para determinar el número óptimo de clusters en K-means. Se basa en analizar cómo cambia la suma de distancias cuadradas intra-cluster (inercia) a medida que aumentamos el número de clusters. El objetivo es identificar un "codo" en la gráfica, donde el decremento de la inercia comienza a ser más lento.
El codo estaría en 3, ya que es el punto donde la pendiente de la curva comienza a disminuir significativamente.
De k = 1 a k = 3, hay una enorme caída de la inercia. Esto indica que agregar más clusters (k) mejora considerablemente la compactación dentro de los grupos.
De k = 3 en adelante, la caida de la inercia es mucho más gradual. Esto indice que agregar más clusters no mejora tan significativamente el modelo.
Con este dataset, entonces, el número óptimo de grupos es de 3.
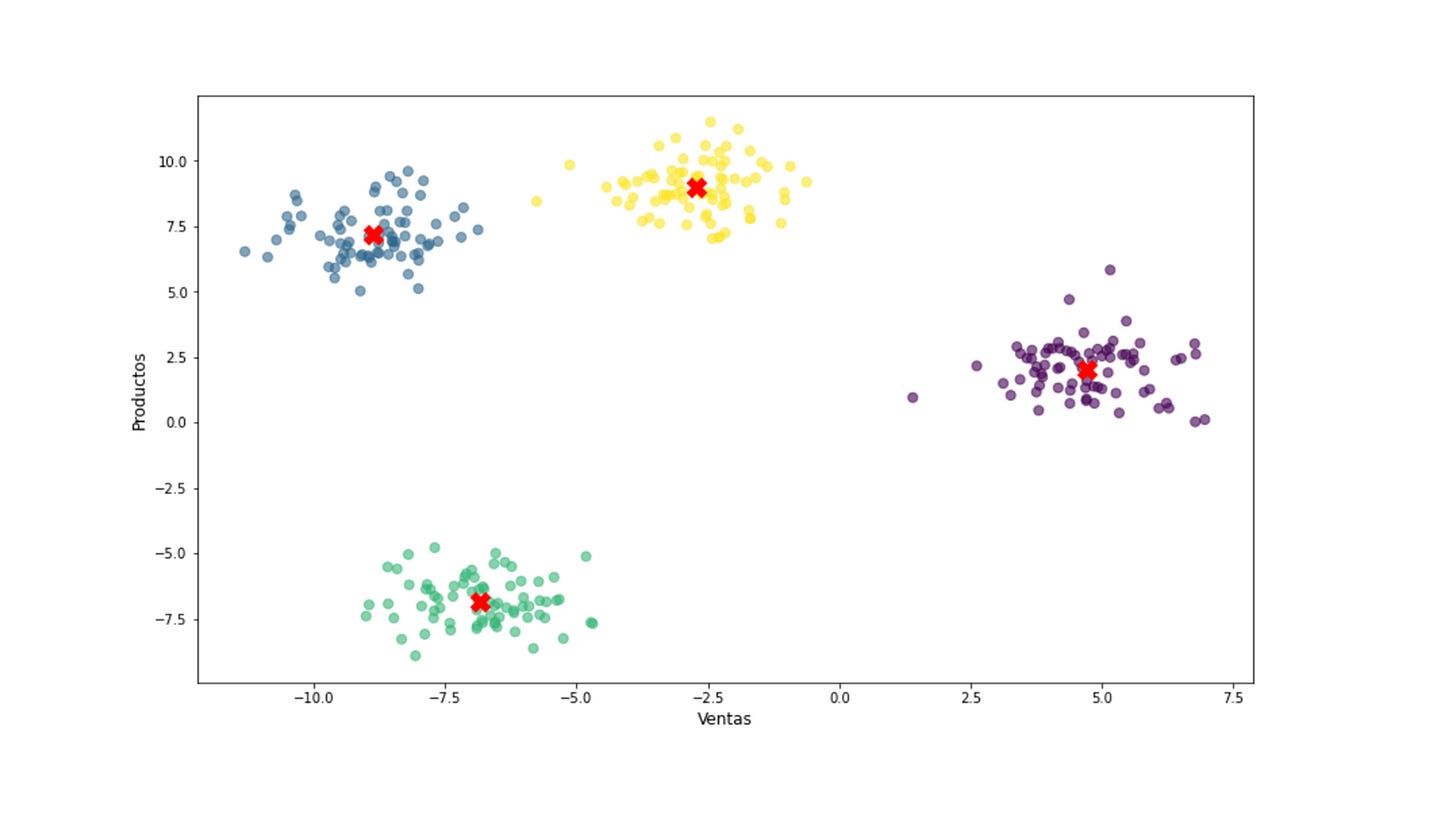
Caso Kaggle
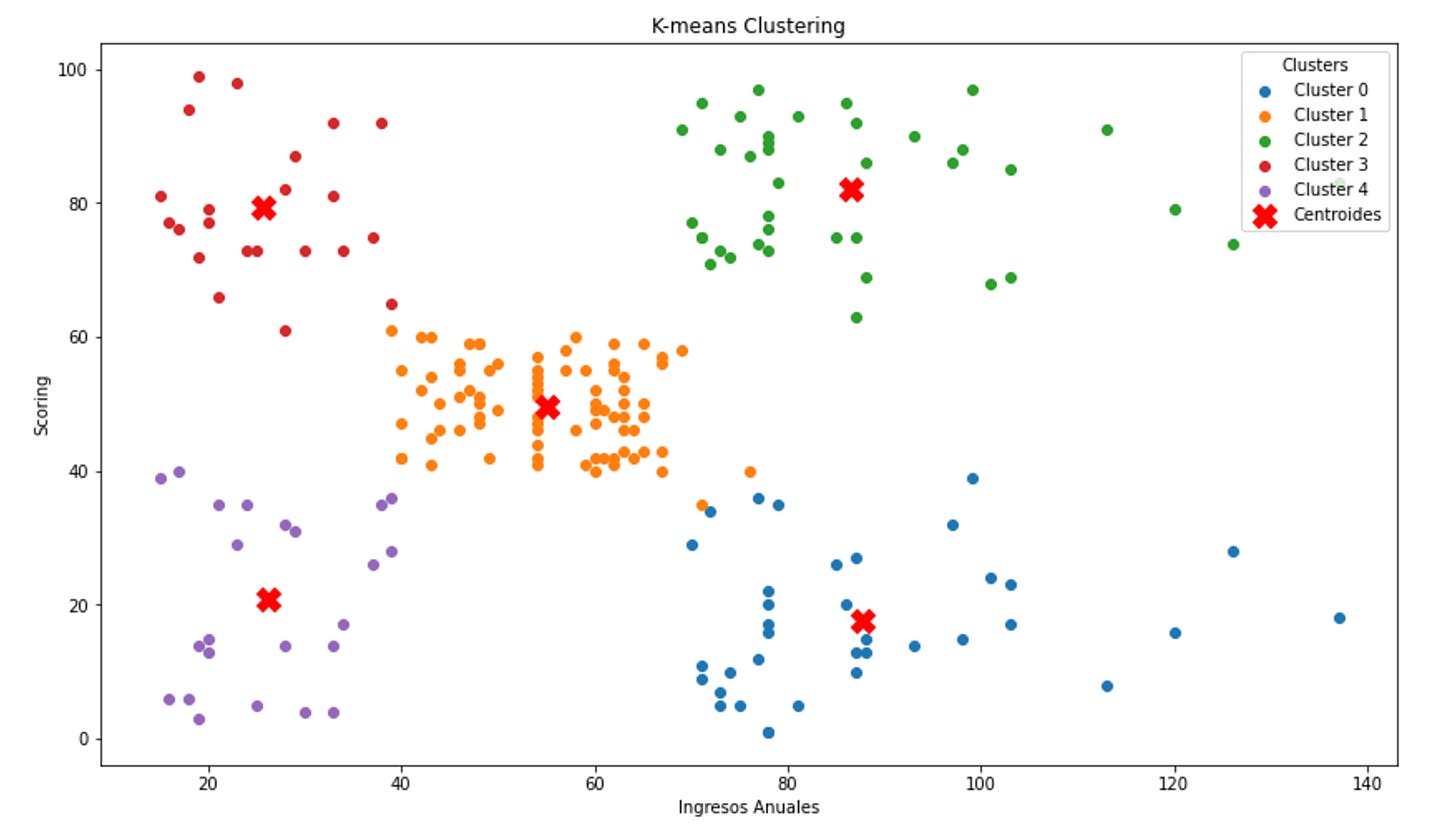
En este dataset puedes descargar un CSV que es el que uso para ejecutar el modelo k-means para encontrar unos sub-grupos a partir, en este caso, del scoring de gasto y los ingresos anuales.
Lógicamente, se han formado 5 grupos a raíz de la ejecución del método elbow y el resultado, ante esas dos variables fue de cinco, como se ve en la siguiente imagen:
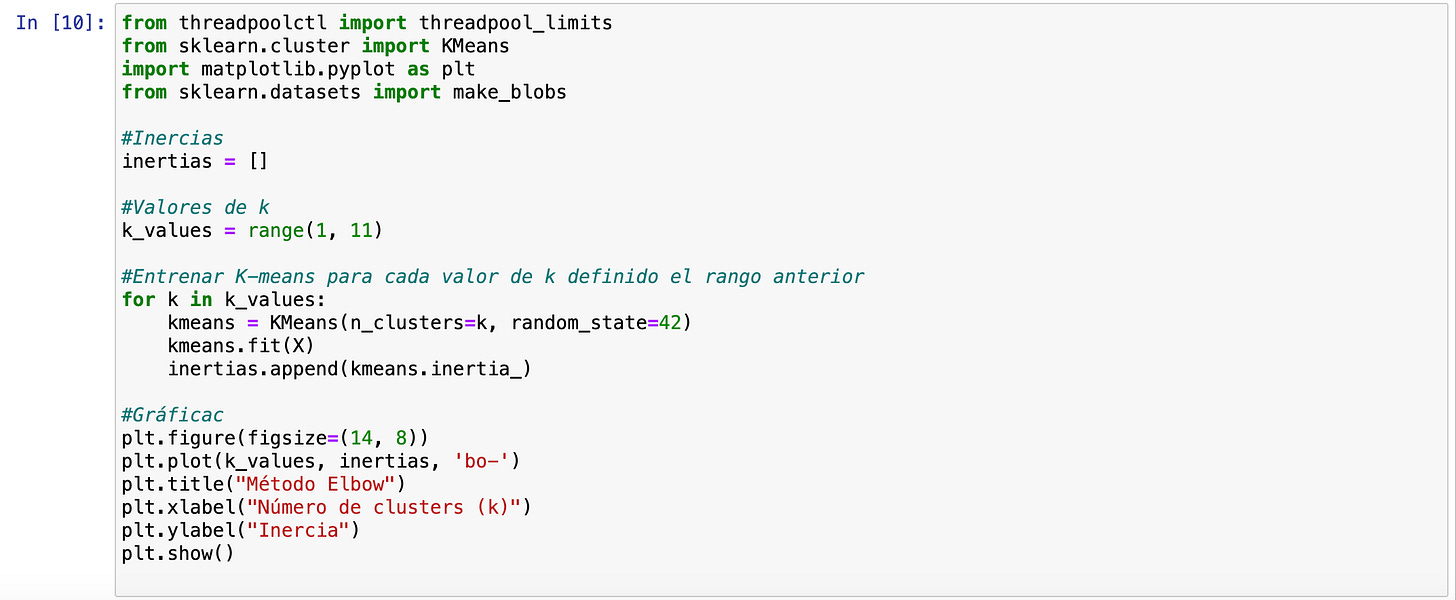
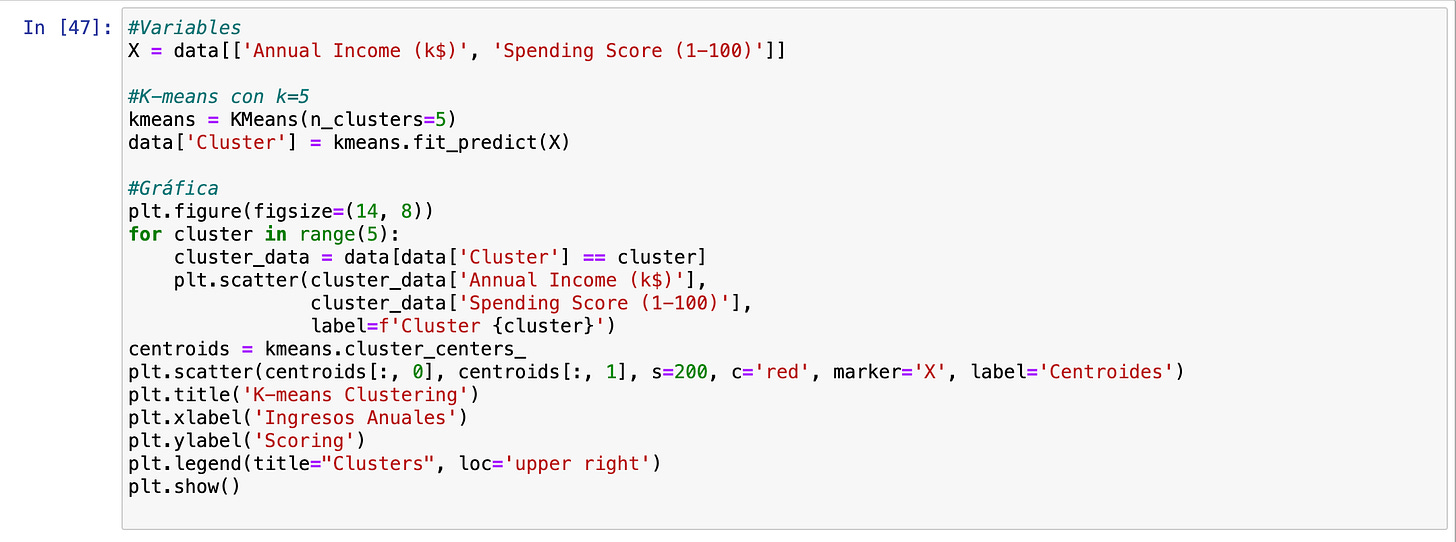
Para ejecutar estos dos elementos, deberíamos ejecutar estos dos códigos:

Evaluación del modelo y Caso GA4
Pero… el modelo debe evaluarse.
No basta con que una gráfica luzca bien.
En esta profesión nada se mide a ojímetro. Todo tiene una métrica, un parámetro: un dato.
Sin embargo, la evaluación del modelo lo mostraré con un caso práctico en Dadadata. Jorge Carrión, gran profesional y mejor persona, ha abierto su Substack a otros profesionales que solemos crear contenido por una buena causa: AYUDAR A VALENCIA POR LA CRISIS DE LA DANA. Este contenido estará solo disponible si te suscribes a su canal (aquí más info sobre esto).
Solo si te suscribes en dadadata (por una buena causa) recibirás el 8 de diciembre de 2024 el contenido sobre evaluación del modelo K-means en el marco de un caso real. Esto es fundamental y es el elemento crítico para dar por bueno un modelo de K-means.
¡Y hasta aquí puedo leer!